Division Mental Math Strategies

We have already discussed mental math strategies for addition and subtraction as well as mental math strategies for multiplication in previous posts. Today we will talk about division strategies that not only help students solve problems quickly but most importantly they help them gain a conceptual understanding of numbers and develop flexible mathematical thinking.

Once your students have understood the concept of division with number lines, pictures, arrays, base ten blocks, and other manipulatives they will be ready to practice some mental math strategies.

Some students discover mental math strategies through practice, naturally, however, most of the students need to be taught the strategies and practice applying them to selected problems. There is a special joy in discovering a strategy, a “trick”. We can guide our students to “discover” a strategy by providing appropriate problems and discussing them.

Many of these strategies are used for simplifying fractions and finding equivalent fractions.

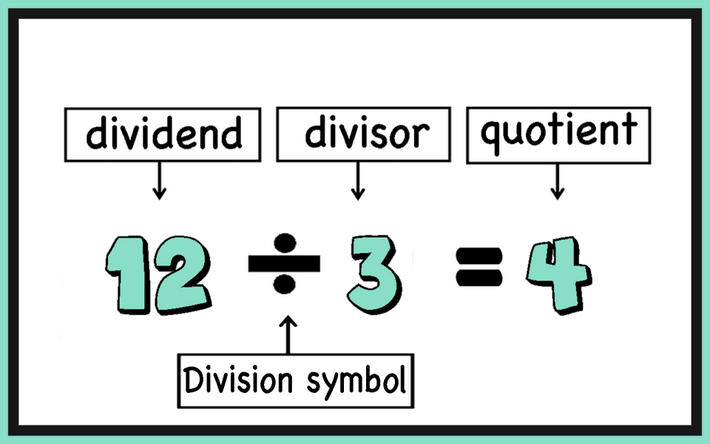
Division Strategies

Like with equivalent fractions (fractions are division after all) we can multiply or divide both the dividend and the divisor with the same number and it will not change the answer. This property allows us to simplify division problems.

Dividing by 5

Since dividing a number by 10 is usually easier to determine, when a number is divided by 5 we can multiply both the dividend and the divisor by 2. This works well with decimals as well.

Halving the dividend and the divisor

When both the dividend and the divisor are even numbers we can half them to get smaller numbers. We can half them more than once.

Dividing by a common factor

If the numbers divided are odd then we can divide them both by a common factor if it is convenient. Even if the numbers are even like above and we can find a common factor and we can divide both by that number to simplify.

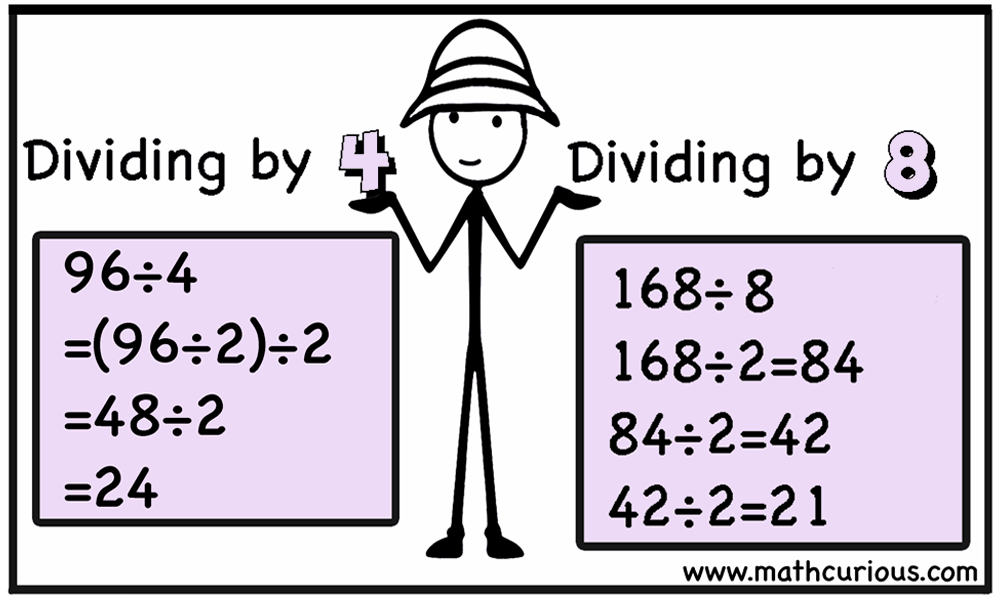
Dividing by 4 and 8

Dividing by 4 is the same as dividing by 2 (halving) twice. Same way dividing by 8 is the same as dividing by 2 three times.

Decomposing the divisor to a product

In this strategy, we decompose the divisor into its factors which means that we write it as a product and then we divide step by step. We follow the order of operations and we divide from left to right.

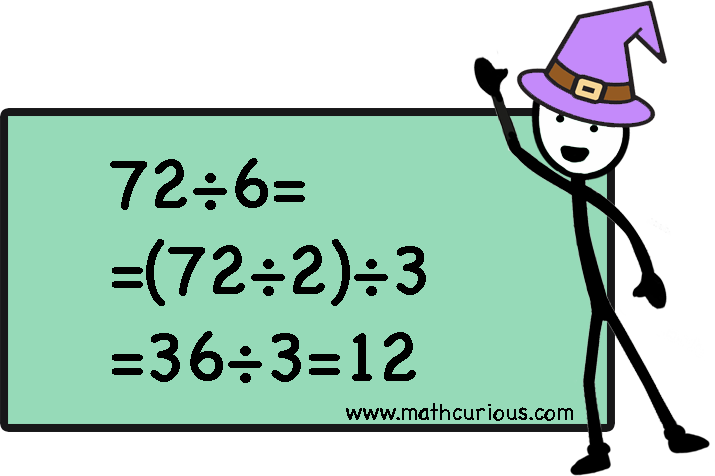
Decompose the dividend to a product

We can also write the dividend as a product and divide step by step. We follow the order of operations and we solve from left to right.

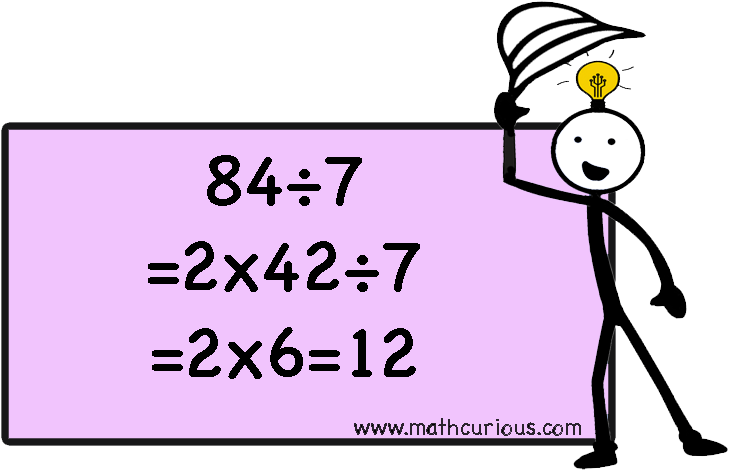
Rounding or compensating

We can round or compensate the dividend to make the division problems simpler.

Dividing Multiples of 10,100,1000

When both the dividend and the divisor are multiples of 10 or 100 or 1000 we can divide them both by their common factor to simplify the problem. As the visual below shows 32 tens divided by 8 tens is the same as 32 ones divided by 8 ones. The answer is 4 in both cases.

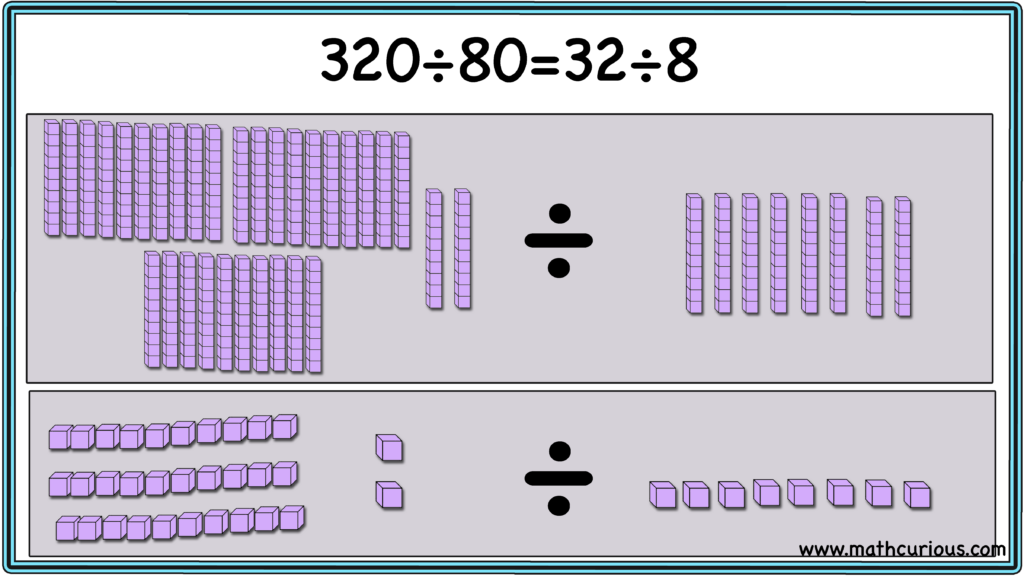
When only the dividend is a multiple of 10,100,1000 we can not divide both by the same factor so we can simplify by decomposing the dividend into its factors.

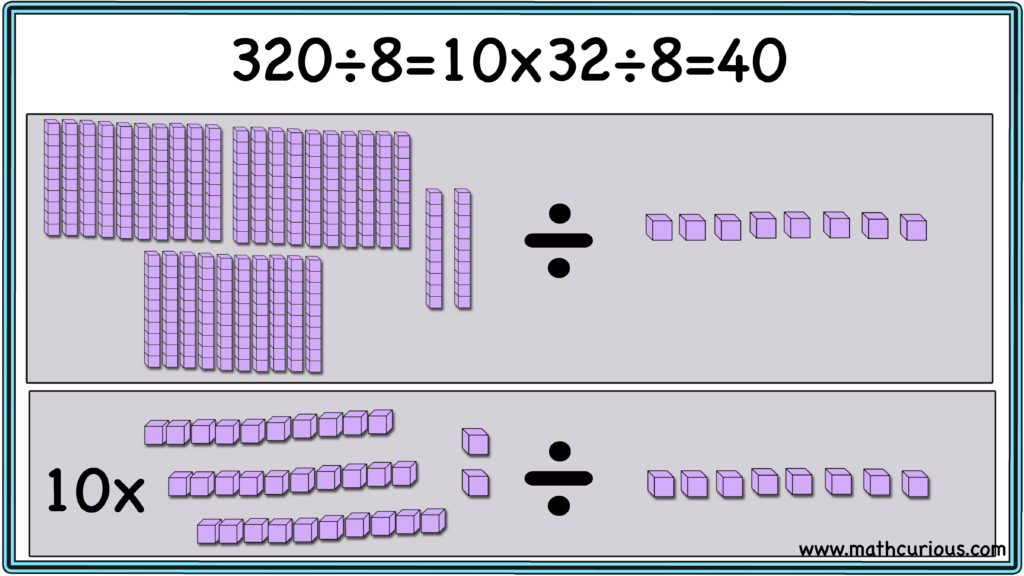
Sometimes we need to use both the strategies above.

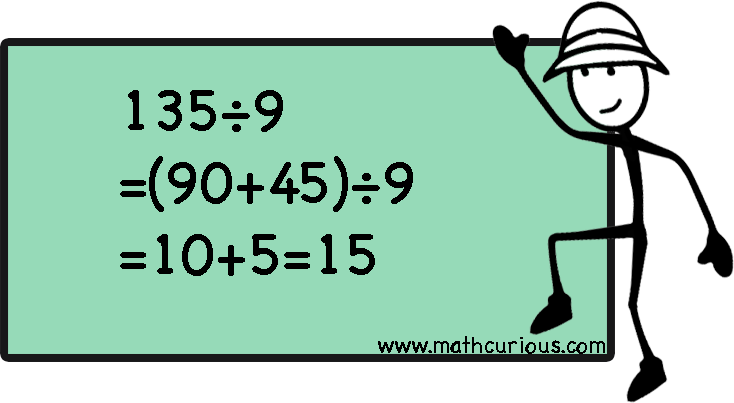
Splitting the Dividend-Partial quotients

We can decompose the dividend into numbers that are “friendlier”, compatible, or divisible by the divisor. This way we get easier and smaller numbers to work with. Then we divide each number and add the quotients. This strategy is also called partial quotients and it is used for greater numbers as well. There are many ways to show our thinking when using the partial quotients strategy. Some are the area model. distributive property, write it as a sum of fractions, and repetitive subtraction.

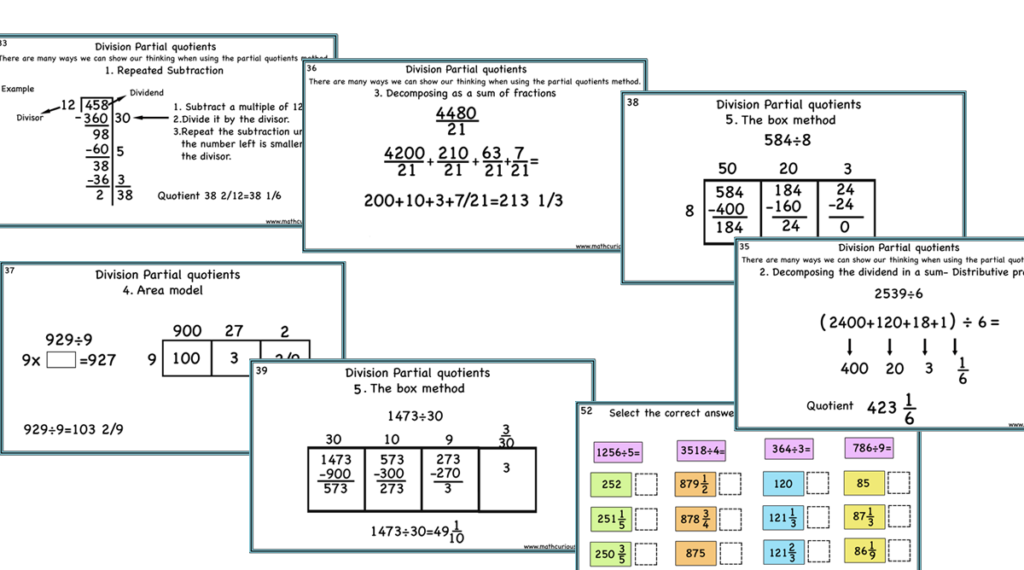
Combining strategies

Combining strategies helps us solve complicated division problems more simply and conceptually. I was never a fan of the long-division traditional algorithm. I love the partial quotients strategy because I have seen how much it helps students with their mental math. Combined with other strategies it makes problems simpler and clear.

I can not stress this enough, students will be successful at learning the strategies and division generally if their multiplication, addition, and subtraction mental skills are strong. They need to be fluent with their multiplication facts to be able to decompose big numbers to use the partial quotients method and see the relations. For example, when a student sees the problem 35420÷70, they should be able to see the multiples of 7 and decompose to (35000+420)÷70. If you are starting with the concept of division or your students need more help understanding division check out Diving into Division -Teaching division conceptually

Mental Math Strategies -Division-Activities

I have created a collection of activity cards to practice the mental math strategies for division as mentioned above. The resource includes visuals, examples, and explanations simplifying division problems, solving division problems, clearing misconceptions, and more.