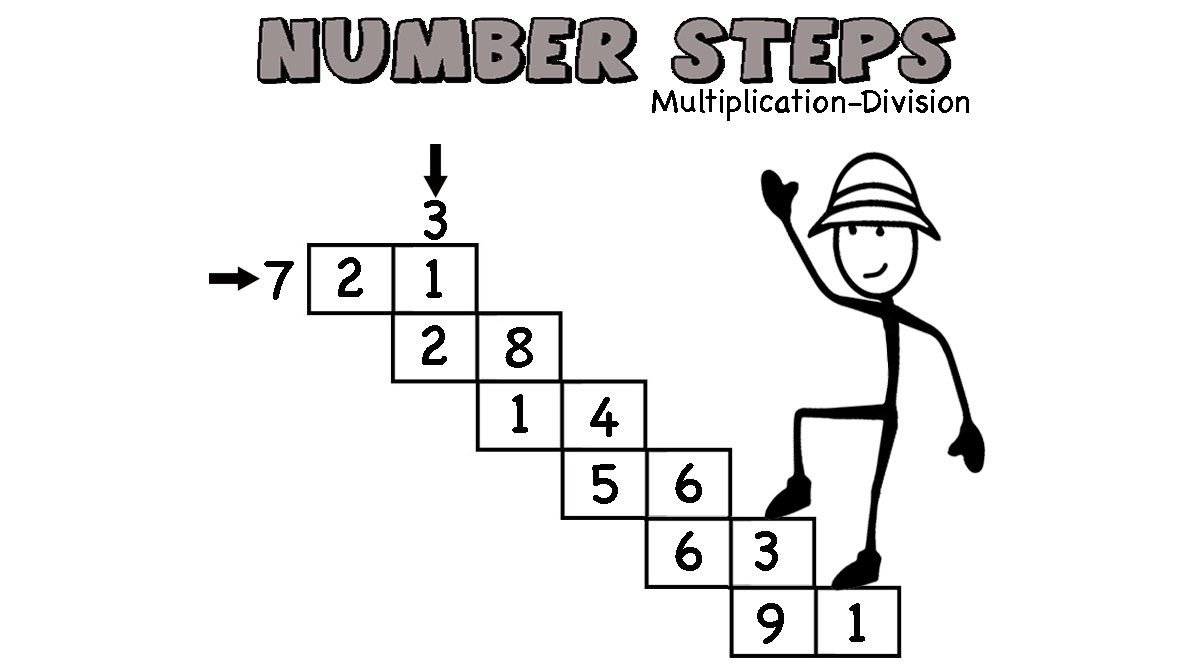
Today we would like to share with you a fun activity we created (my little mathematicians and I) to challenge my youngest son with multiplication facts practice. We call them the Number Steps! This is a great activity to challenge your students with. I use this activity to challenge my advanced learners when we do multiplication fact practice.
Grades 3 and up
With numbers steps, you need to fill in single-digit numbers to form two-digit numbers horizontally and vertically that intersect, based on the instructions.
Here is an example:

Here is one of the answers
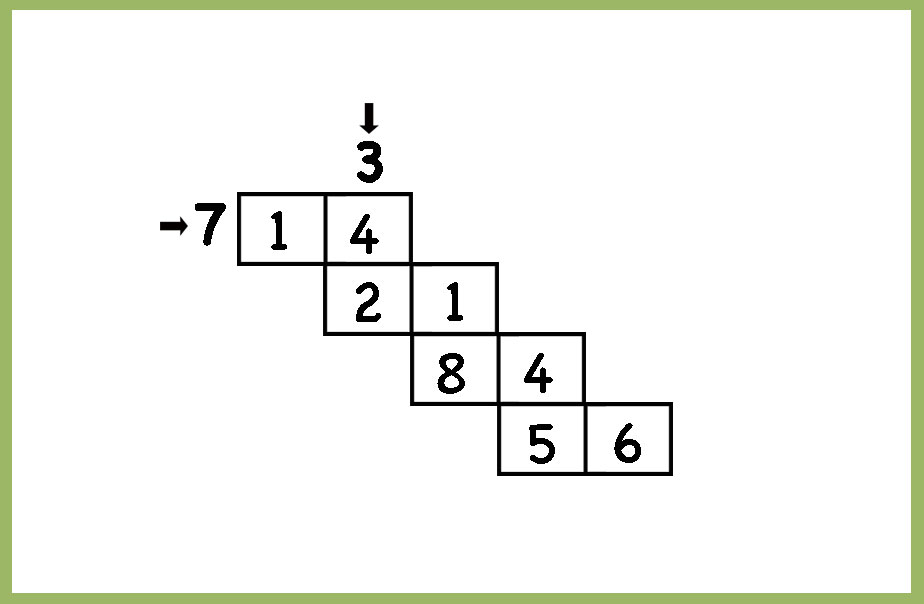
and here is another one
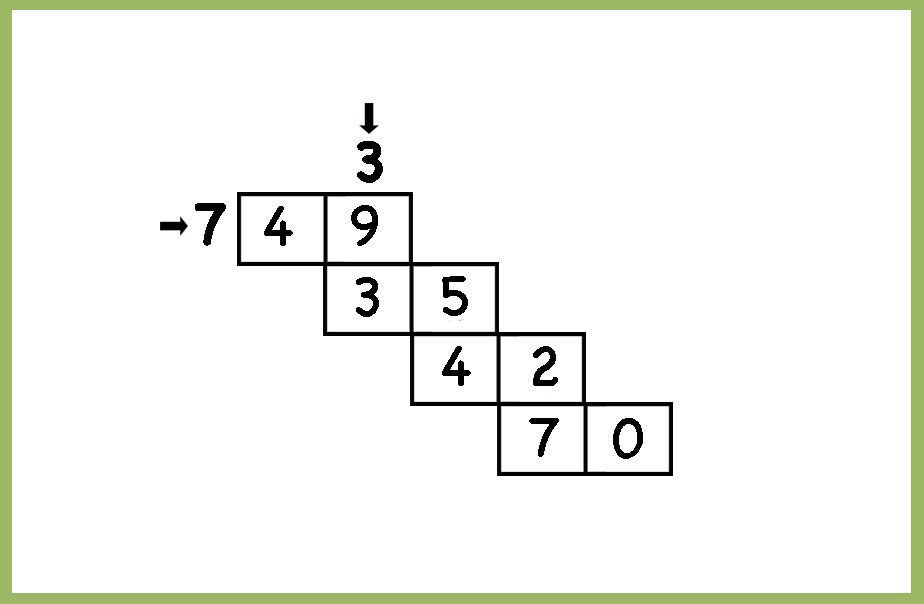
We really enjoyed creating the problems and solving them. This works well because the question feels like a puzzle, and it encourages problem-solving. It is a good practice for recalling multiplication facts for sure, but it is also great practice for divisibility rules. For the example above, starting from up you choose a multiple of 7. (49) The last digit of that number is the first digit for the multiple of 3. Which numbers are divisible by 3 that have 9 in the 10s. 91,92,93…divisibility rules! 93. Now which number with 3 at the ten’s place is a multiple of 7? And so on.
Another example, and one of the answers.
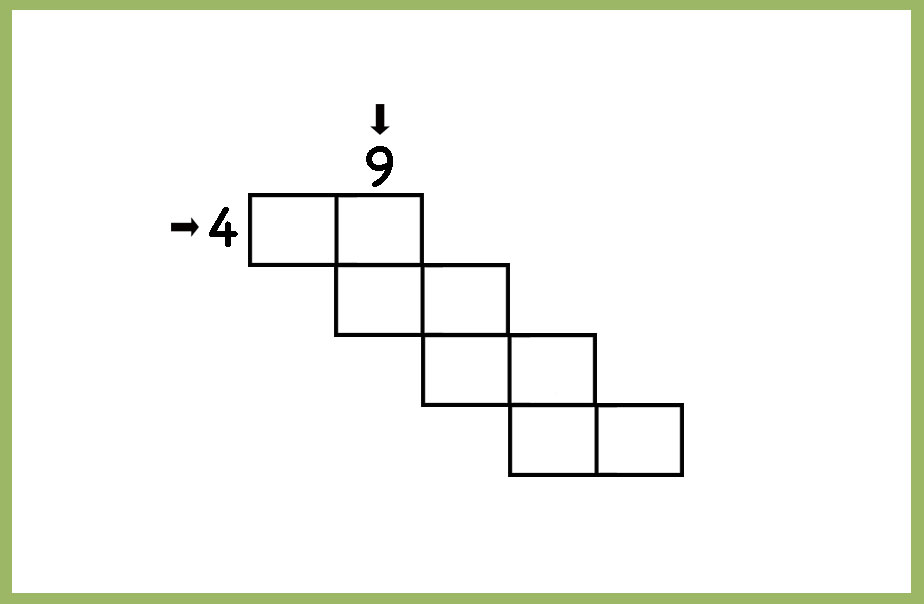
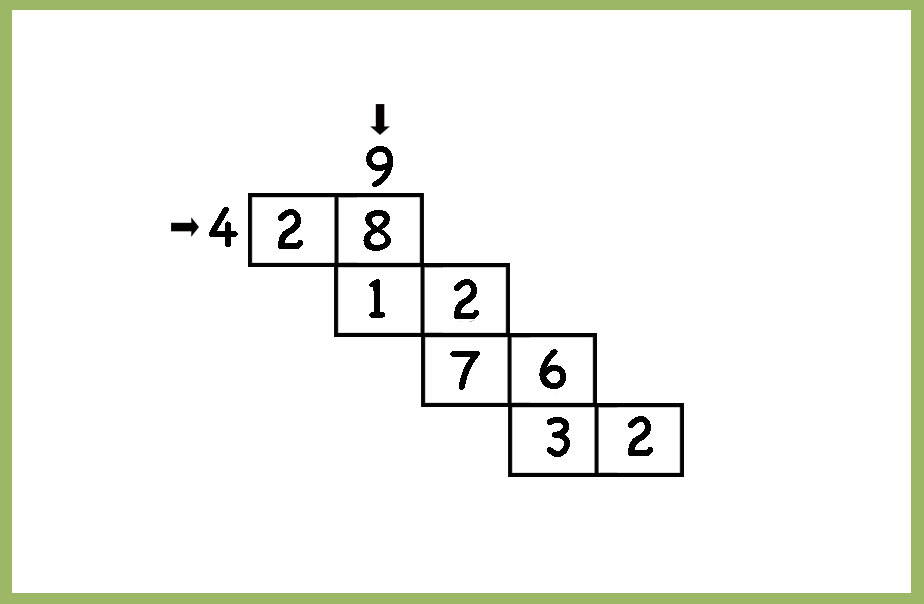
The steps can be more or less based on the desired level of difficulty. The numbers you choose as factors horizontally and vertically also affect the level of difficulty. It is important, that you choose the factors ( horizontally and vertically) carefully and solve the problem yourself first. Multiples of, for example, 5 end with 5 or 0 and it is difficult to make the multiples of the other number always starting with a 5. ( cannot start with 0). 10 will not work as a factor for this activity. Fewer steps and easier factor pairs like 2 and 4 are less challenging and great to start with.
Challenge your students to continue the steps as far as they can without repeating the two-digit numbers.
Here are some Number-Steps worksheets to solve. There is more than one answer for each problem, one answer provided for each.
Let us know what you think of this idea. Does it work for your students?