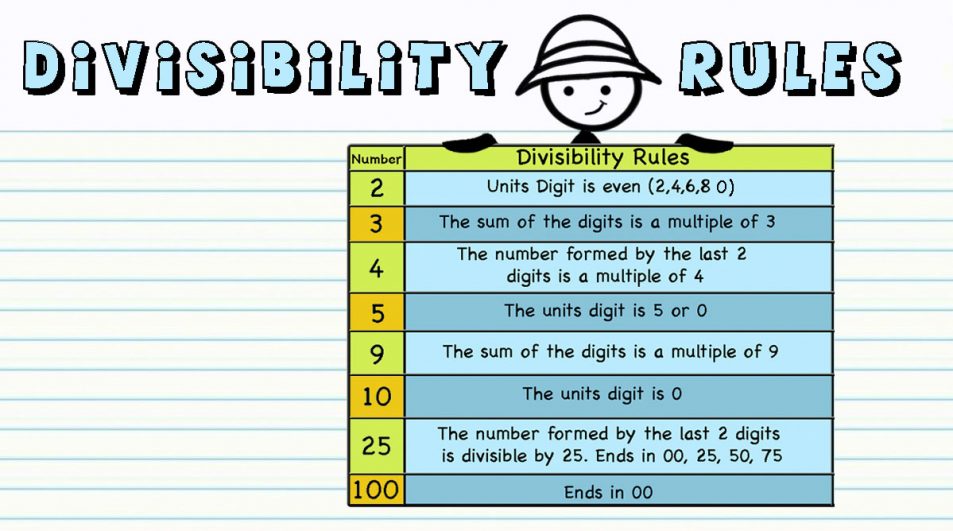
Divisibility Rules help us figure out if a number is divisible by 2, 3, 4, 5, 9, 10, 25 and 100. They help us perform a divisibility test easily and quickly. Students usually know the factors of the numbers 1-100 by grade four from practicing the multiplication facts. Divisibility rules help them with greater numbers. Before presenting the divisibility rules lead students (if possible) to discover them through discussions (using smaller numbers) or ask them to explain/prove a rule. You can have very interesting math discussions and get the students thinking.
The rules of divisibility also help us figure out if a number is prime.

A number that has more than two factors is called a composite number.
Divisibility Test for 2
A number is divisible by 2 when its last digits are 0, 2, 4, 6, or 8. For example, the number 236 is an even number (divisible by 2) because its last digit is 6 which is even. We only need to look at the last digit because the we know that the tens and hundreds of the number are even (2×5). The ones digit, however, needs to be tested. For example, the number 237 is not divisible by 2 because when divided by 2 it will leave a remainder of 1. 7 is not an even number.
Divisibility Test for 3 and 9
A number is divisible by 3 if the sum of its digits is a multiple of 3.
For example, 561 is a multiple of 3 because the sum of its digits is 12 which is a multiple of 3. But how did this rule came to be? Every 10 can be replaced by 9+1 and every 100 can be replaced by 99+1 so our number 561 can be written as 5x(1+99) + 6x(1+9) +1 which becomes
5+ (5×99) + 6 + (6×99) +1.
The product in the brackets is a multiple of 3 since is one of the factors is 99 and 9 which are also multiples of 3. So what we need to test is the sum 5 + 6 + 1. This is the sum of the digits of the number we started with. So by adding the digits of the number we can tell if a number is a multiple of 3.
The same logic is applied for the divisibility test for 9. If the sum of the digits of a number is a multiple of 9 then the number is divisible by 9.
Divisibility Test for 4
A number is divisible by 4 if the last 2 digits form a multiple of 4. The reason we only test the last two digits is that one hundred is a multiple of 4 (4×25) so every multiple of 100 will be a multiple of 4 as well. 100s, 1000s, 10 000s and so on do not have to be tested. However, 10s and 1s need to be tested. 10 is not a multiple of 4 but 20 and 48 are, so are 32 and 12. The number formed by the last 2 digits tells us if the number is a multiple of 4.
Divisibility Test for 5
A number is divisible by 5 if its last digit is 0 or 5.
We only need to test the 1s digit because we know that 10 is a multiple of 5 and therefore so are 100, 1000 and so on. 344 can be written as 300+40+4 = (3×100)+(4×10)+4. 344 is not multiple if 5.
Divisibility Test for 10
A number is divisible by 10 if the 1s digit is o. This means that the number only has 10s, 100s, 1000s and so on, all of them multiple of 10. If the number has any 1s then it will leave a remainder when divided by 10.
Divisibility Test for 25
A number is divisible by 25 if the last 2 digits are 00, 25, 50, or 75.
If the last 2 digits are 00 then the number has no 10s and 1s, it is only “made” with 100s. We know that 100 is divisible by 25 (4×25) therefore so is 1000 (10×100) , 10000 (100×100) and so on. We need to make sure that the number formed by the last two digits is a multiple of 25. The only two-digit numbers multiple of 25 are 25, 50, 75.
Here are the main divisibility rules.
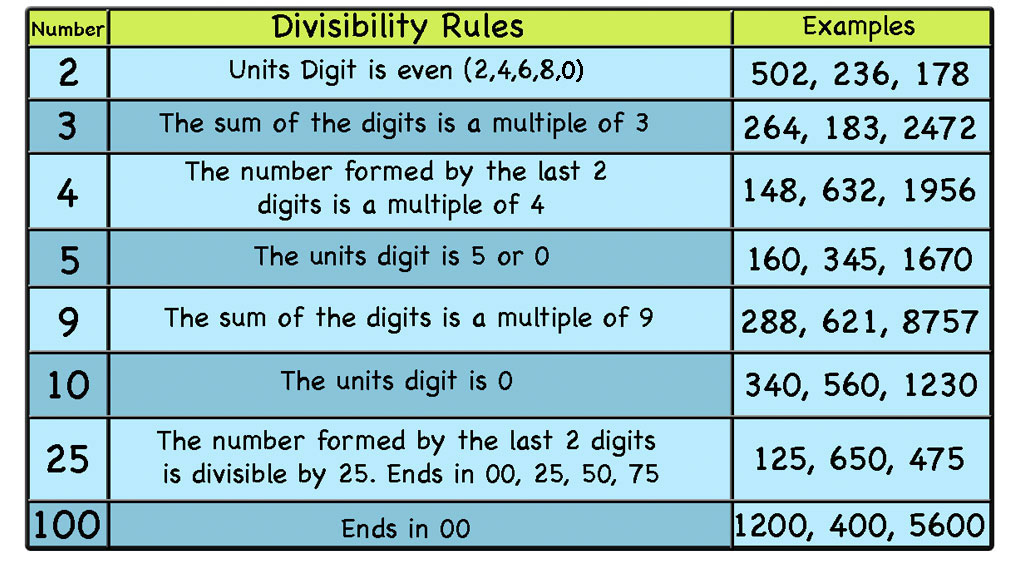
We haven’t mentioned how to check divisibility for 6, 7 and 8.
Divisibility Test for 6
The prime factors of 6 are 2 and 3. So for a number to be divisible by 6, it must also be divisible by 2 and 3. Therefore, we need to check if a number is even and then check if the sum of the digits is a multiple of 3.
Divisibility Test for 7
Seven is a prime number so we cannot test the divisibility by 7 using other numbers like in the case of 6. So what we need to do is check the combinations of its digits to see if they form multiples of 7. For example, 637 is a multiple of 7 because I can break it to 630 +7. Both 630 (7x9x10) and 7 are multiples of 7. Another example is 14 560. I can write the number as 14000+560 = 2 x 7 x 1000 + 8 x 7 x 10. How about 15358. I can write the number like this 15000 + 350 + 8 =14000+1000 +350 +8. I know that 14000+350 is divisible by 7. I need to test 1008. Number 98 is a multiple of 7 so 980 is a multiple as well. I can write 1008 as (980 +20) +8 = 980 + 28. 28 is a multiple of 7 so the number 15358 is a multiple of 7. Some number are a bit complicated to figure out.
There is also an interesting formula for checking divisibility by 7 which was discovered by Chika Ofili, a 12-year-old boy. According to Mary Ellis, Ofili’s teacher and the Mathematics head at Westminster Under School where Ofili attends, Ofili discovered the formula while doing his holiday homework contained in a book called First Steps for Problem Solvers.
Let’s try with the number 3465
Step 1. Take away the last digit and double it. We get 10.
Step 2. Subtract the result from the new number formed (without the ones digit.) 346-10 = 336
You can repeat the same procedure until you reach a small enough number to be able to tell if it is divisible by 7.
So let’s continue. 336 take away the 6 and double it. It becomes 12 so 33-12 = 21 which is a multiple of 7. Therefore 3465 is a multiple of 7.
Divisibility Test for 8
Since 100 and 10 are not divisible by 8 we need to check if the number formed by the last 3 digits is a multiple of 8. For example, 1224 is a multiple of 8 since 224 is a multiple of 8. 6356 is not a multiple of 8 because 356 is not divisible by 8. Also, a number cannot be divisible by 8 if it is not divisible by 2 and 4. So unless a number is divisible by 2 and 4 we don’t need to check for divisibility by 8.
How to tell if a number is prime.
If a number is prime then its only factors are itself and 1, so there is no need to look for more factors. For example, if a number is not divisible by 2, this means that it is not divisible by any even number, so half the numbers are tested. If a number is not divisible by 3 then it is not divisible by the multiples of 3 either. By testing with the numbers 2, 3, 5, 7, 11, 13, and other smaller than the number itself primes we can cover all their multiples as well. So we can be sure whether our number is a prime or not.
Geogebra has this great tool for visualizing divisibility.
We have created some print and digital (google slides) activities for practicing divisibility rules.



Google slides

Find the free and premium version of the resource below.
The premium version includes 36 printable task cards, 36 interactive slides/task cards and 2 worksheets