In today’s post, we will talk about factorization. What it is. How it is done. How it helps us and how to help students understand it. We will dive deep into these with an example for factors of 24.
Factoring is a math operation. It is the process of breaking a number into smaller numbers that multiplied together, give us the original number. Those numbers are called Factors. In other words, we can write the original number as a product of these smaller numbers.
Example: Factors of 24
For example, I can write 24 as the product of 6 and 4. In this case, 6 and 4 are factors of 24. When multiplied together they give us 24.
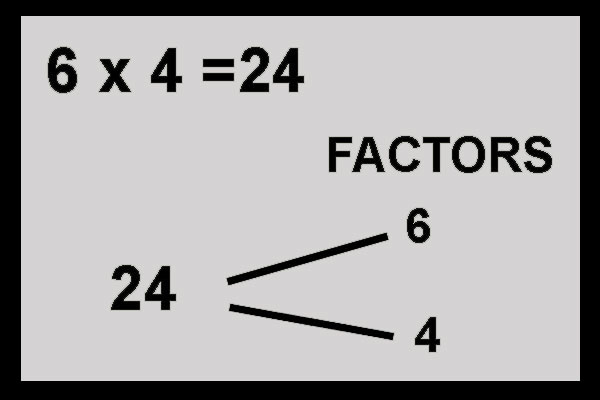
Of course, there are more factors of 24. 1 is always a factor of any number and the number itself is a factor too, since 1 x 24 = 24
Factoring is like being given the answer to a multiplication problem and then having to figure out what that problem was. When students know their multiplication facts well they can easily figure out the factors of a number.
A good way to help students find factors is by using the multiplication table.
What other factors of 24 are there?
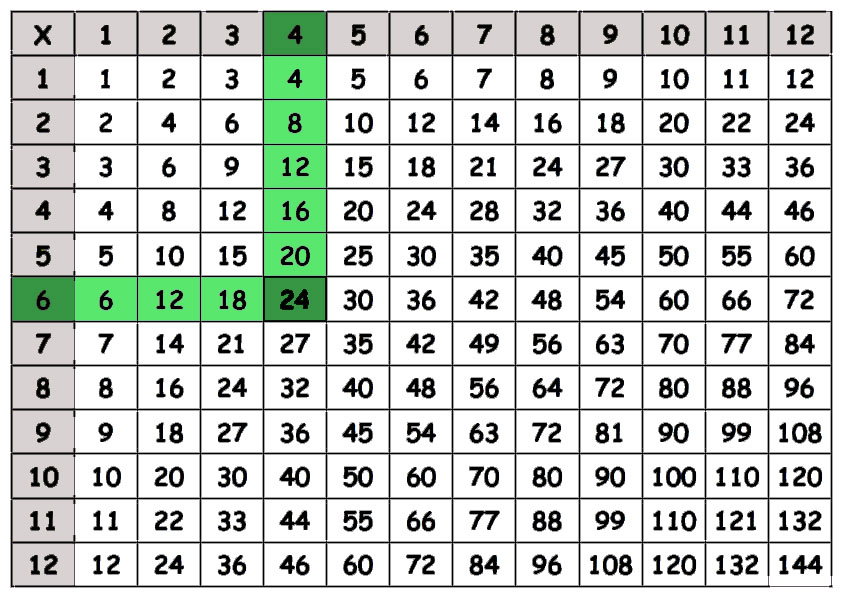
When we look for 24 on the multiplication table we will find more factors.
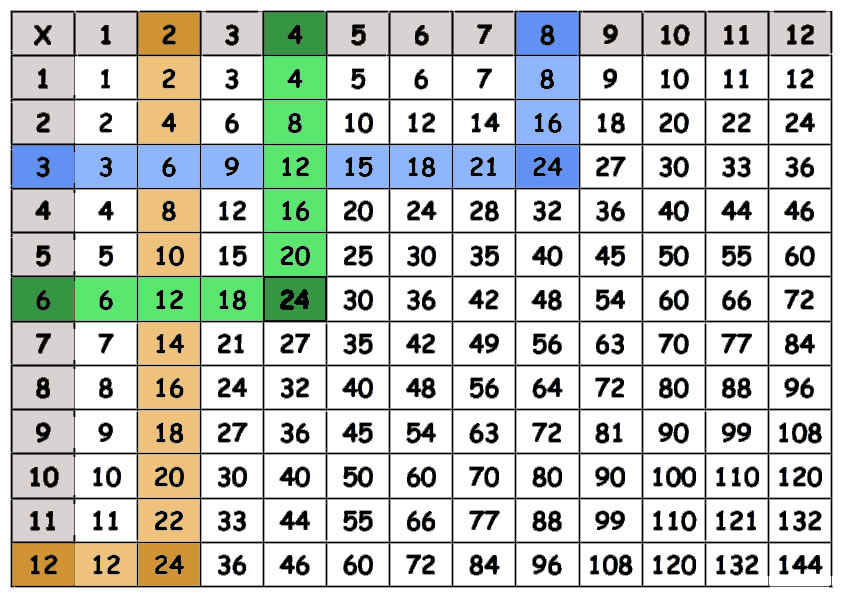
As we can see there is more than one way to factor a number.
1×24, 6×4, 3×8, and 2×12 are equal to 24, therefore, 1, 24, 6, 4, 2, 12, 3 and 8 are all factors of 24. This means that each of these numbers divide evenly into 24.

When I divide 24 by one of its factors the answer (quotient) is a whole number or an integer, which means that there is no fractional or decimal part. In other words, dividing a number by its factor will leave no remainder.
Testing for divisibility
A way to check if a number is a factor is to test its divisibility. There are 3 ways we can do that.
- Count by that number and see if at some point you reach the requested number. For example, is 6 a factor of 18? Let us count by 6 and see if we can reach 18. 6, 12, 18, 24, …. 3 x 6 =18, so 6 is a factor of 18 and so is 3. Since the factors come in pairs, when we find a factor, we also find its pair. Now let’s try to see if 7 is a factor of 18. 7, 14, 21, … I never stop at 18 which means that 7 is not a factor of 18.
- Look for remainder. If we divide 18 by 6 the answer is 3 but if we divide 18 by 7 the answer is 2 and a remainder of 4. If the division leaves a remainder it means that the number tested is not a factor.
- Use a calculator. Try the same division using a calculator. If the answer is a decimal number then that number is not a factor.
What if we need to find all the factors of a number?
Since the factors come in pairs we only need to test half the numbers 1-24. Remember. Every time we find a factor we also find its pair. Another factor!
So let’s write down all the numbers 1-12
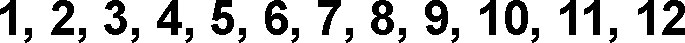
We know that number 1 is always a factor and so is the number itself. 1×24=24
So 1 and 24 are our first factors.
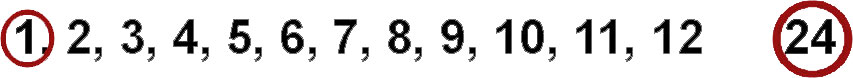
Since 24 is an even number 2 is a factor too. 2 x 12 gives us 24 so we know that we don’t have to test 12. So we got two more factors 2 and 12.
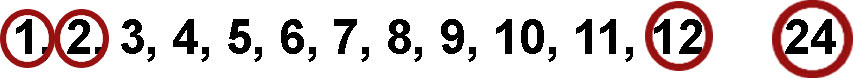
As we saw before 3 is a factor of 24. (3 x 8 =24). If we use the multiplication table and go through the numbers in the line of 3 (vertically or diagonally) we will find 24. This means that 24 is a multiple of 3 which makes 3 a factor of 24. 3 multiplies with 8 to make 24 so 8 is a factor of 24 too.

As we saw before, using the multiplication table 4 x 6=24 so both 6 and 4 are multiples of 24.

We have already tested 7 and if we do a test by counting by 7, using the table, or using the calculator, we will again see that 7 is not a multiple of 24. The same goes for 9, 10 and 11

So we found all the factors of 24.
You can do the activity above in a rainbow shape to show the pairing of the factors.
Once children learn the multiplication facts well they will be able to find factors of numbers without doing all this work. However, it is important to know and understand what factoring is and to be able to do a divisibility test.
Why do we need to know how to factor?
Factoring allows us to solve word problems like the following ones.
- Helen is preparing goodie bags for her friends. She has 24 chocolates and 40 lollypops and she wants to use all of them. What is the smallest number of chocolates and lollypops she can put in each bag and how many bags will she prepare?
- I want to plant 45 sunflower plants, 81 tulip plants and 63 daisy plants in my garden. If I put the same number of plants in each row and each row has only one type of plant, what is the greatest number of plants I can put in one row?
Factoring is very useful when simplifying fractions or finding equivalent fractions. It helps find the greatest common factor to divide the numerator and denominator and get a simpler fraction.
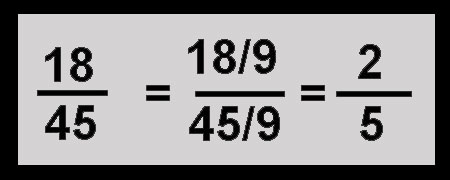
The greatest common factor of 18 and 45 is 9. When I divide both the numerator and denominator with 9, I get the simplest equivalent fraction
Factoring can be used to solve polynomial inequalities, quadratic equations, and simplify expressions to be able to solve them. Of course, students learn algebraic equations at high school. However, the foundation for that is built through their elementary years and factoring is a very important skill.
Here is a worksheet to practice factors with your students.